What Is Focal Length In Camera Lens

Measure of how strongly an optical system converges or diverges light

"Rear focal altitude" redirects hither. For lens to film altitude in a camera, see Flange focal altitude.

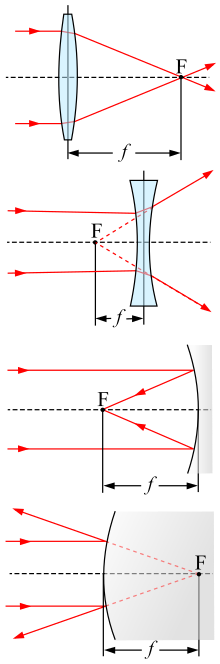
The focal point F and focal length f of a positive (convex) lens, a negative (concave) lens, a concave mirror, and a convex mirror.

The focal length of an optical system is a measure of how strongly the system converges or diverges calorie-free; it is the inverse of the arrangement's optical power. A positive focal length indicates that a system converges light, while a negative focal length indicates that the system diverges low-cal. A system with a shorter focal length bends the rays more sharply, bringing them to a focus in a shorter altitude or diverging them more quickly. For the special case of a sparse lens in air, a positive focal length is the altitude over which initially collimated (parallel) rays are brought to a focus, or alternatively a negative focal length indicates how far in forepart of the lens a bespeak source must be located to form a collimated axle. For more general optical systems, the focal length has no intuitive significant; it is simply the inverse of the organization's optical power.

In nearly photography and all telescopy, where the subject is essentially infinitely far away, longer focal length (lower optical ability) leads to higher magnification and a narrower bending of view; conversely, shorter focal length or higher optical power is associated with lower magnification and a wider bending of view. On the other hand, in applications such as microscopy in which magnification is achieved by bringing the object close to the lens, a shorter focal length (higher optical power) leads to higher magnification because the discipline tin can be brought closer to the center of projection.

Thin lens approximation [edit]

For a thin lens in air, the focal length is the distance from the center of the lens to the principal foci (or focal points) of the lens. For a converging lens (for case a convex lens), the focal length is positive and is the distance at which a beam of collimated lite will exist focused to a single spot. For a diverging lens (for example a concave lens), the focal length is negative and is the distance to the point from which a collimated beam appears to be diverging after passing through the lens.

When a lens is used to form an image of some object, the distance from the object to the lens u, the altitude from the lens to the image v, and the focal length f are related by

${\displaystyle {\frac {1}{f}}={\frac {1}{u}}+{\frac {one}{v}}\ .}$

The focal length of a thin convex lens can be easily measured by using it to form an image of a distant light source on a screen. The lens is moved until a sharp image is formed on the screen. In this instance 1 / u is negligible, and the focal length is and then given by

${\displaystyle f\approx five\ .}$

Determining the focal length of a concave lens is somewhat more hard. The focal length of such a lens is considered that indicate at which the spreading beams of lite would meet before the lens if the lens were not there. No image is formed during such a test, and the focal length must be determined past passing light (for example, the light of a light amplification by stimulated emission of radiation axle) through the lens, examining how much that light becomes dispersed/ bent, and following the beam of calorie-free backwards to the lens'southward focal signal.

General optical systems [edit]

For a thick lens (one which has a non-negligible thickness), or an imaging organisation consisting of several lenses or mirrors (due east.yard. a photographic lens or a telescope), the focal length is often called the effective focal length (EFL), to distinguish it from other commonly used parameters:

• Front focal length (FFL) or front focal altitude (FFD) (s _F) is the distance from the front focal indicate of the organisation (F) to the vertex of the first optical surface (Due south₁).^{[ane] [two]}
• Back focal length (BFL) or back focal distance (BFD) (southward′ _F′) is the distance from the vertex of the last optical surface of the arrangement (S_ii) to the rear focal point (F′).^{[1] [2]}

For an optical system in air, the effective focal length (f and f′) gives the altitude from the front end and rear principal planes (H and H′) to the corresponding focal points (F and F′). If the surrounding medium is non air, then the distance is multiplied by the refractive index of the medium (n is the refractive index of the substance from which the lens itself is made; north ₁ is the refractive alphabetize of whatever medium in forepart of the lens; due north ₂ is that of any medium in dorsum of information technology). Some authors telephone call these distances the front/rear focal lengths, distinguishing them from the front/rear focal distances, defined above.^[1]

In general, the focal length or EFL is the value that describes the power of the optical organisation to focus calorie-free, and is the value used to calculate the magnification of the system. The other parameters are used in determining where an image will exist formed for a given object position.

For the case of a lens of thickness d in air ( n ₁ = n ₂ = i), and surfaces with radii of curvature R _ane and R ₂, the effective focal length f is given by the Lensmaker'due south equation:

${\displaystyle {\frac {ane}{f}}=(north-i)\left({\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-ane)d}{nR_{1}R_{2}}}\correct),}$

where n is the refractive alphabetize of the lens medium. The quantity 1 / f is likewise known as the optical power of the lens.

The corresponding front end focal distance is:^[3]

${\displaystyle {\mbox{FFD}}=f\left(one+{\frac {(north-1)d}{nR_{2}}}\right),}$

and the back focal altitude:

${\displaystyle {\mbox{BFD}}=f\left(1-{\frac {(n-one)d}{nR_{ane}}}\right).}$

In the sign convention used here, the value of R ₁ volition be positive if the offset lens surface is convex, and negative if it is concave. The value of R ₂ is negative if the 2nd surface is convex, and positive if concave. Note that sign conventions vary betwixt different authors, which results in unlike forms of these equations depending on the convention used.

For a spherically curved mirror in air, the magnitude of the focal length is equal to the radius of curvature of the mirror divided past ii. The focal length is positive for a concave mirror, and negative for a convex mirror. In the sign convention used in optical design, a concave mirror has negative radius of curvature, and so

${\displaystyle f=-{R \over 2},}$

where R is the radius of curvature of the mirror'due south surface.

See Radius of curvature (optics) for more than information on the sign convention for radius of curvature used here.

In photography [edit]

28 mm lens

fifty mm lens

seventy mm lens

210 mm lens

An instance of how lens choice affects angle of view. The photos above were taken by a 35 mm photographic camera at a fixed distance from the subject.

Images of blackness letters in a thin convex lens of focal length f are shown in reddish. Selected rays are shown for letters East, I and K in blue, green and orangish, respectively. Note that East (at 2f) has an equal-size, existent and inverted epitome; I (at f) has its image at infinity; and K (at

f / 2 ) has a double-size, virtual and upright epitome.

In this reckoner simulation, adjusting the field of view (past changing the focal length) while keeping the subject in frame (by changing appropriately the position of the photographic camera) results in vastly differing images. At focal lengths approaching infinity (0 degrees of field of view), the lite rays are about parallel to each other, resulting in the discipline looking "flattened". At pocket-size focal lengths (bigger field of view), the subject appears "foreshortened".

Camera lens focal lengths are usually specified in millimetres (mm), but some older lenses are marked in centimetres (cm) or inches.

Focal length (f) and field of view (FOV) of a lens are inversely proportional. For a standard rectilinear lens, FOV = 2 arctan ten / 2f , where x is the diagonal of the film.

When a photographic lens is set to "infinity", its rear nodal bespeak is separated from the sensor or film, at the focal airplane, by the lens's focal length. Objects far away from the camera and so produce precipitous images on the sensor or film, which is also at the image plane.

To render closer objects in abrupt focus, the lens must be adjusted to increase the distance between the rear nodal bespeak and the picture, to put the pic at the image plane. The focal length (f), the altitude from the front end nodal signal to the object to photograph (s ₁), and the distance from the rear nodal point to the image aeroplane (southward ₂) are and then related by:

${\displaystyle {\frac {one}{s_{one}}}+{\frac {1}{s_{two}}}={\frac {i}{f}}.}$

Every bit due south ₁ is decreased, s ₂ must be increased. For example, consider a normal lens for a 35 mm camera with a focal length of f = fifty mm. To focus a afar object (s ₁ ≈ ∞), the rear nodal point of the lens must be located a distance s ₂ = fifty mm from the prototype plane. To focus an object 1 grand abroad (s ₁ = 1,000 mm), the lens must be moved two.6 mm farther away from the epitome airplane, to s _ii = 52.six mm.

The focal length of a lens determines the magnification at which it images afar objects. Information technology is equal to the distance betwixt the image plane and a pinhole that images afar objects the aforementioned size as the lens in question. For rectilinear lenses (that is, with no prototype distortion), the imaging of distant objects is well modelled as a pinhole camera model.^[4] This model leads to the simple geometric model that photographers apply for calculating the bending of view of a camera; in this case, the angle of view depends only on the ratio of focal length to film size. In full general, the angle of view depends too on the distortion.^[5]

A lens with a focal length almost equal to the diagonal size of the film or sensor format is known as a normal lens; its angle of view is like to the angle subtended by a big-enough print viewed at a typical viewing distance of the print diagonal, which therefore yields a normal perspective when viewing the print;^[six] this angle of view is almost 53 degrees diagonally. For full-frame 35 mm-format cameras, the diagonal is 43 mm and a typical "normal" lens has a 50 mm focal length. A lens with a focal length shorter than normal is often referred to equally a wide-angle lens (typically 35 mm and less, for 35 mm-format cameras), while a lens significantly longer than normal may be referred to equally a telephoto lens (typically 85 mm and more, for 35 mm-format cameras). Technically, long focal length lenses are merely "telephoto" if the focal length is longer than the physical length of the lens, but the term is frequently used to describe whatsoever long focal length lens.

Due to the popularity of the 35 mm standard, camera–lens combinations are often described in terms of their 35 mm-equivalent focal length, that is, the focal length of a lens that would have the aforementioned bending of view, or field of view, if used on a total-frame 35 mm photographic camera. Use of a 35 mm-equivalent focal length is especially common with digital cameras, which oftentimes use sensors smaller than 35 mm moving-picture show, and then crave correspondingly shorter focal lengths to achieve a given angle of view, by a factor known every bit the crop gene.

See also [edit]

• Depth of field
• Dioptre
• f-number or focal ratio

References [edit]

1. ^ ^{a b c} John E. Greivenkamp (2004). Field Guide to Geometrical Optics. SPIE Press. pp. half-dozen–ix. ISBN978-0-8194-5294-8.
2. ^ ^{a b} Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley. p. 168. ISBN978-0805385663.
3. ^ Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley. pp. 244–245. ISBN978-0805385663.
4. ^ Charles, Jeffrey (2000). Applied astrophotography . Springer. pp. 63–66. ISBN978-ane-85233-023-1.
5. ^ Stroebel, Leslie; Zakia, Richard D. (1993). The Focal encyclopedia of photography (3rd ed.). Focal Printing. p. 27. ISBN978-0-240-51417-8.
6. ^ Stroebel, Leslie D. (1999). View Camera Technique. Focal Press. pp. 135–138. ISBN978-0-240-80345-6.

Source: https://en.wikipedia.org/wiki/Focal_length

Posted by: leeholoy1948.blogspot.com

Share this post